- As described in [Bale et al., 2008], the electrical design of the STEREO/Waves antenna and preamplifier circuit is represented as the following figure (see sect. 3):
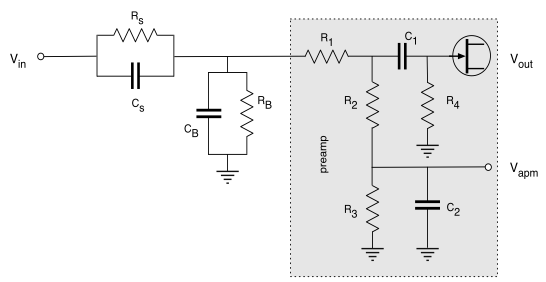
with the following values for the circuit elements:
This study also mention the following measured quantities (see sect. 5):Name Component Value Note Sheath resistance Rs ~ 0.75MΩ Antenna capacitance Cs ~ 40pF Base resistance Rb ~ 1-10MΩ Base capacitance Cb ~ 60pF C1 100pF C2 100pF R1 100Ω R2 33MΩ R3 33MΩ R4 150MΩ
with Cs = Cb + Cc + Cpa . Finally, this study also mention a base capacitance used for the rheometric analyses (see sect. 6.1):Name Component Value Note Cable capacitance Cc ~ 13pF Base capacitance Cb ~ 32pF Preamplifier capacitance Cpa ~ 22pF Stray capacitance Cs ~ 67pF Used by [Oswald et al., 2009]. Name Component Value Note Base capacitance Cb 90pF - A second study [Eastwood et al., 2009] gives the value of the stray capacitance for monopoles and dipoles, using the galactic noise:
Name Component Value Note Stray capacitance (monopole) Cs,m ~ 80-90pF Used by [Macher et al., 2007]. Stray capacitance (dipole) Cs,d ~ 40pF - A third study [Zouganelis et al., 2010] gives the value of the base capacitance of the hXY dipole, using the shot noise:
Name Component Value Note Base capacitance (dipole) Cb 32pF ± 4pF
STEREO/Waves antenna Quick Facts
Electrical design
Receiver Noise
- An interesting byproduct of the calibration proposed by [Zaslavsky et al., 2011] is the receiver noise level (V2noise).
(1) see this document (PDF) for detailed information.Spacecraft DF-mode (1) Antenna V2noise (dB) STEREO-A 31 hXY -160.9 STEREO-A 31 hZ -162.8 STEREO-A 13 hX -161.8 STEREO-A 13 hYZ -161.6 STEREO-A 11 hX -163.0 STEREO-A 11 hZ -162.7 STEREO-A 12 hX -163.1 STEREO-A 12 hY -162.4 STEREO-A 21 hY -163.4 STEREO-A 21 hZ -162.8 STEREO-B 31 hXY -162.4 STEREO-B 31 hZ -165.9 STEREO-B 13 hX -163.2 STEREO-B 13 hYZ -164.2 STEREO-B 11 hX -163.4 STEREO-B 11 hZ -165.8 STEREO-B 12 hX -163.4 STEREO-B 12 hY -166.4 STEREO-B 21 hY -163.9 STEREO-B 21 hZ -165.7
Nota Bene:
- results for modes 13 and 31: [Zaslavsky et al., 2011]
- results for modes 11, 12 and 21: personal communication by A. Zaslavsky, calibration done on day 2009-01-01.
Credits
This web page has been compiled and is maintained by B. Cecconi1, Co-I of STEREO/Waves.
Special thanks to: C. Briand1, V. Krupar1,2, M. Maksimovic1, M. Panchenko3, A. Zaslavsky1.
1. LESIA, Observatoire de Paris, Meudon, France;
2. Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic;
3. Space Research Institute, Austrian Academy of Sciences, Graz, Austria.
Special thanks to: C. Briand1, V. Krupar1,2, M. Maksimovic1, M. Panchenko3, A. Zaslavsky1.
1. LESIA, Observatoire de Paris, Meudon, France;
2. Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic;
3. Space Research Institute, Austrian Academy of Sciences, Graz, Austria.
For any comments, inputs or suggestion, please contact B. Cecconi.
Last update:
January 22 2015 19:51:29.